Confidentialité différentielle : résolvez 5 énigmes pour comprendre ce concept cher à Apple

Au moment de la WWDC 2016, Apple sortait tout juste de sa bataille contre le FBI au sujet du chiffrement et s’érigeait désormais en chevalier blanc de la vie privée. Mais quand l’expression « differential privacy » s’est retrouvée projetée en grand sur l’écran de la keynote, beaucoup de sourcils se sont levés. Lors de son implémentation dans iOS 10, cette notion était bien obscure, si ce n’est accueillie avec suspicion : récolter encore plus de données tout en prétendant garantir la vie privée des utilisateurs, what could go wrong?

récolter encore plus de données tout en prétendant garantir la vie privée, what could go wrong?

D’autant que les explications de Craig Federighi, VP de l’ingénierie logicielle, n’étaient pas des plus claires pour les néophytes. Trois concepts bien différents étaient mis dans le même sac :

• le hachage, la forme non-réversible couramment utilisée en cryptographie pour stocker les mots de passe en sécurité ;
• le sous-échantillonage, c’est-à-dire ne se baser que sur une partie des données ;
• et l’injection de bruit, la seule de ces trois notions à entrer en soi dans le champ de la confidentialité différentielle, et que nous expliquerons au cours de cet article.

En dévoilant le HomePod à la WWDC 2017, Apple a réitéré son attachement à la vie privée — argument marketing fort face aux produits d’Amazon et de Google, qui peuvent susciter l’inquiétude quand on sait l’intérêt qu’ont ces groupes dans l’exploitation des données personnelles. Cette fois, Apple a mis en avant le chiffrement et l’anonymisation des données transmises. Alors certes, ce genre d’activités ne rentre pas dans le business model de la firme fruitée. Mais il reste tout à fait légitime de s’interroger sur la vraie nature de cette confidentialité différentielle, qui n’est en fait pas si hypocrite que certains ont pu le croire.

Nous tâcherons de tout vous faire comprendre avec de petites énigmes. On vous encourage évidemment à tout lire pour saisir les différentes facettes du concept, mais si vous n’avez pas le temps, la n°3 est celle qui résume véritablement les fondamentaux.

Énigme n°1 : le prix Netflix

En 2007, Netflix offrait un prix de 1 million de dollars à quiconque trouverait le meilleur moyen d’améliorer son algorithme de suggestion de films. Il avait ainsi donné une base de données d’entraînement aux développeurs participants. Chez lui, Netflix stockait explicitement les noms de ses utilisateurs avec les films qu’ils regardent et les notes qu’ils donnent ; mais pour la compétition, il a bien évidemment supprimé les noms, pensant que l’anonymat de ses membres serait ainsi préservé.

Grossière erreur ! Arvind Narayanan et Vitaly Shmatikov, de l’université du Texas à Austin, se sont emparés de la base de données « anonymisée » et ont réussi à deviner non seulement le nom de certains utilisateurs, mais même aussi parfois leur affiliation politique ! À votre avis, comment ont-ils fait ? Réflechissez un peu avant de regarder la solution, sous cette image.

Indice : l’Internet est vaste.

Réponse: les deux chercheurs se sont rendus sur le site de notation de films IMDb, qui contient des données non anonymes. En regardant les dates où tel utilisateur d’IMDb avait noté tel film, ils n’ont eu qu’à chercher dans les tables anonymisées de Netflix qui avait vu ces films à ces dates-là. Ce qui a beaucoup joué dans l’efficacité de cette méthode, c’est le fait que deux profils Netflix n’ont jamais plus de 50 % de ressemblance, et qu’il n’a donc fallu que 50 % de similitude pour déterminer le profil IMDb correspondant.

Netflix n’avait pas utilisé de confidentialité différentielle : voilà le résultat. En suivant cette méthode, des universitaires ont pu déanonymiser partiellement des dossiers médicaux, entre autres choses beaucoup plus sensibles. Nous n’arriverons donc pas tout de suite à la differential privacy mais étudierons d’abord un cas d’école, situé un peu en amont et qui sera utile pour la partie théorique.

Énigme n°2 : 😀

Nous nous permettrons de reprendre cet exemple aussi stupide que génial imaginé par le cryptographe Matthew Green de l’université Johns Hopkins. Supposons qu’Apple, pour un grand projet secret sur lequel il vaut peut-être mieux ne rien savoir, veuille connaître la proportion de ses clients avides de l’émoji 😀 sur iMessage.

L’app iMessage analyserait les messages passés de l’utilisateur et lui attribuerait une note 1 s’il utilise 😀 au-delà d’un certain seuil, et 0 sinon. Chaque iPhone enverrait alors cette information d’un bit à Cupertino sous forme d’un rapport chiffré (interceptable mais indéchiffrable). Là-bas, on ne stockerait pas « on a reçu un rapport contenant la note 0 à telle heure », mais « on a reçu un rapport à telle heure, et à cette heure-ci la somme de toutes les notes est de 6 309 802 ». La base de données est complètement anonyme mais peut fuiter. Ça a l’air plus sécurisé que tout à l’heure, mais il y a encore une faille ! Saurez-vous la retrouver ?

Indice : c’est un peu tiré par les cheveux, mais si vous avez bien compris l’énigme précédente, ça ne devrait pas être difficile.

Solution : en espionnant ce qui entre et sort de l’iPhone, des hackeurs pourraient déterminer quand le rapport est arrivé à Cupertino. Une fois les bases de données d’Apple leakées, ils pourraient trouver la somme de toutes les notes à ce moment-là, soit 6 309 802. Regardant la ligne juste avant, ils verraient soit exactement le même nombre (c’est-à-dire que l’utilisateur de l’iPhone espionné n’est pas avide du fameux émoji), soit 6 309 801 (auquel cas ses messages en sont saupoudrés).

Vous pouvez d’ores et déjà vous préparer à l’énigme suivante en imaginant un moyen de combler cette faille, rendue plus saillante par l’artificialité de cet exemple. En attendant, vous êtes maintenant prêts à passer par un peu de théorie.

Un peu de théorie, maintenant

Le principe de la differential privacy, ou DP, est le suivant : faire en sorte que peu importe que vos informations personnelles soient récoltées ou non, ça n’aura aucune incidence notable sur ce qu’on pourra apprendre sur vous.

Car même si vous ne participez pas à l’étude, elle laissera deviner des choses sur votre personne. Supposons dans l’exemple précédent que vous êtes un détenteur d’iPhone : si l’étude d’Apple est dévoilée et qu’il apparaît que 80% des utilisateurs iOS sont friands de cet émoji, vos collègues sous Android pourront glousser, même si vous avez refusé que vos données à ce sujet soient collectées.

Évidemment, si tous les utilisateurs refusent de voir leurs données récupérées, l’étude n’est pas publiée et cela a une grosse incidence sur ce qu’on peut apprendre d’eux. Mais rappelez-vous le calcul différentiel, les dérivées et les intégrales vus au lycée ; car c’est là que le mot « différentiel » prend tout son sens. En additionnant chaque goutelette d’eau insignifiante que représentent les données de chaque utilisateur, on vise à obtenir un océan de données exploitables.

CC Maria Eklind

On peut ainsi expliquer formellement pourquoi l’exemple décrit dans l’énigme précédente ne remplit pas les conditions d’une DP parfaite. Si vous êtes noté 1, le fait que cette donnée soit collectée augmentera de 1 la somme stockée dans la base de données. Mais dans un cas idéal de DP, que vos données à vous soient récupérées ou non, ça ne doit rien changer. De facto, cette utopie n’est pas pratique et on essaye de minimiser la fuite de confidentialité (c’est à dire, ici, ce +1 que vos données rajoutent dans la base) en-dessous d’une valeur epsilon ? arbitraire.

Cette notion de confidentialité différentielle a été déterminée par Cynthia Dwork, chercheuse chez Microsoft (oui, cette entreprise à l’appétit vorace pour les données de ses utilisateurs), qui a écrit avec ses collègues un article précurseur en 2006. La prochaine énigme est basée sur l’exemple décrit par Dwork dans sa publication ; c’est une technique connue depuis un demi-siècle, à laquelle elle apporte de nouvelles perspectives.

Prêts à faire de la vraie DP ?

Énigme n°3 : « Avez-vous déjà violé la loi ? »

Prenons un groupe de personnes, dont certaines ont déjà commis des délits et d’autres non. On veut connaître la proportion de délinquants dans le groupe. Hors de question de demander bêtement à chacun « avez-vous déjà violé la loi ? », car personne ne se dénoncera ! À votre avis, comment pourra-t-on estimer le nombre de délinquants dans le groupe (pour peu que celui-ci soit suffisamment grand), mais d’une manière qui n’implique à personne d’être démasqué personnellement ?

Indice : dans le monde réel, vous pourriez leur demander de glisser la réponse dans une urne ; mais en informatique cela reviendrait à l’énigme précédente. Non, vous devrez trouver une autre solution, et elle implique une pièce de monnaie.

Solution : on donne la pièce de monnaie à chaque personne et on lui demande de jouer à pile ou face en cachette. Si c’est face, la personne doit répondre la vérité. Si c’est pile, elle doit relancer la pièce pour choisir de dire « oui » ou « non » à pile ou face. Les délinquants n’auront donc plus peur de se dénoncer, vu que des innocents se « dénonceront » aussi. On a donc alors :

• une moitié de gens qui aura répondu « oui » et « non » à 50/50 ;
• et une moitié de gens qui aura dit la vérité.

Par exemple, si vous prenez 1 000 personnes, 500 d’entre elles répondront à pile ou face et 250 diront donc « oui » sans que cela ne représente de quelconque réalité. Donc, sur vos 1 000 personnes, si 400 personnes vous répondent « oui », vous saurez que 150 d’entre elles font partie de la moitié qui dit la vérité. Multipliez par deux, et vous obtenez que votre groupe contient environ 300 crapules.

Voici donc ce dont parlait Craig Federighi sur la scène d’Apple avec le terme d’« injection de bruit». Évidemment, en vrai, on ne demande pas aux utilisateurs de smartphones de lancer des pièces. Lorsque leurs (vraies) données sont récoltées, celles-ci sont badigeonnées de bruit aléatoire. Quand elles arrivent dans les bases de données, on sait qu’une certaine proportion d’entre elles sont à côté de la plaque, sans savoir lesquelles le sont ou pas. En procédant comme ci-dessus, on arrive ainsi à connaître les données de ces utilisateurs dans leur ensemble, mais pas individuellement car on les a rendues toutes floues.

Ce bruit n’est pas anodin, comme on le verra dans l’énigme suivante. Cette dernière porte sur le machine learning, une discipline où la confidentialité différentielle est source d’applications prometteuses.

Énigme n°4 : Machine learning

En 2014, Matthew Fredrikson et son équipe de l’université du Wisconsin travaillaient sur le dosage de la warfarine, un anticoagulant utilisé pour traiter les thromboses et les embolies pulmonaires. À l’aide d’une base de données publique reliant les résultats de dosages de warfarine à certains marqueurs génétiques, ils ont développé grâce au machine learning un modèle capable de prédire les dosages nécessaires dans telle ou telle situation.

Le modèle est ensuite testé avec des patients virtuels, qu’elle traite de fait aussi bien que ce qui se passe à l’hôpital. Néanmoins, les dossiers médicaux de ces malades imaginaires pouvaient en l’état être lus comme des livres ouverts, et les chercheurs ont décidé que mettre de la differential privacy ne ferait pas de mal sur des informations aussi sensibles (c’était en fait là le but de leur étude).

Que se passe-t-il si on rajoute de la DP ?

Indice : c’est directement lié à la manière dont la confidentialité différentielle fonctionne, et c’est… comment dire…

CC Alex Dodd

Le modèle se met à tuer ses patients. Enfin, quelques-uns.

Tout comme le principe d’incertitude de Heisenberg ne permet de connaître correctement que la position ou la vitesse d’une particule en même temps, la confidentialité et la précision ne vont pas de concert :

• soit le modèle reçoit les informations nécessaires pour traiter correctement ses patients, mais il fait alors fuiter beaucoup d’informations sensibles ;
• soit le « budget » de confidentialité est beaucoup plus exigeant — et le modèle, aveuglé, donne à ses patients des dosages complètement inadaptés.

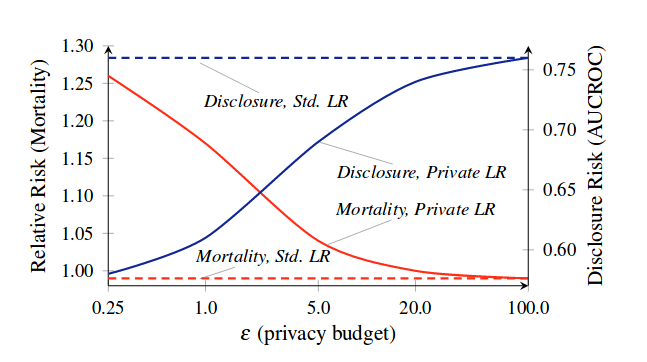
En rouge, la mortalité relative ; et en bleu, le risque de voir des données personnelles compromises. Les tirets correspondent à une situation sans confidentialité.

Dans le monde réel, la DP n’est jamais parfaite. Chaque requête (interaction) sur la base de données fait fuiter un peu de confidentialité, comme les vieux joints d’un tuyau dès qu’on ouvre le robinet. Il n’existe malheureusement pas d’éponge différentielle, et si on continue trop, la fuite peut se transformer en petite inondation. Pour préserver les données, il faut alors jeter et remplacer tout ce qui a été atteint — c’est-à-dire détruire la base. Plus on doit faire de requêtes, plus l’injection de bruit doit donc être importante en compensation. Ce n’est pas dramatique pour des smartphones, mais on voit bien le problème que cela cause sur des applications plus vitales.

Après ces remarques qu’il faut garder en mémoire, passons à la dernière énigme avec une implémentation concrète de confidentialité différentielle. Vous y êtes presque !

Énigme n°5 : OK, Google…

Vous souvenez-vous de l’exemple de Dwork avec les délinquants ? Cette méthode est déjà utilisée par Google depuis 2014 pour collecter des statistiques sur son navigateur Chrome ; la firme de Mountain View l’a adaptée en un système nommé RAPPOR.

Vous savez maintenant, dans les grandes lignes, comment implémenter de la DP sur des données numériques. Cela inclut des questions à réponse fermée, qui équivalent littéralement à des 1 et des 0 comme dans l’énigme de l’émoji. Mais Google veut connaître les adresses des sites visités par ses utilisateurs Chrome, et ce sont des chaînes de caractères, pas des nombres ! Ce ne serait pas raisonnable de modifier aléatoirement les lettres à l’intérieur… Comment s’y prend-il ?

Indice : rappelez-vous de ce que Craig Federighi disait à la WWDC d’Apple.

CC Keso

Avec une bonne dose de hachage ! Le procédé est nettement plus complexe que pour chiffrer un mot de passe. Il utilise des filtres de Bloom, une structure de données mise au point en 1970.

Imaginez un mur de briques blanches et un groupe d’algorithmes de hachage armés chacun d’un pot de peinture jaune. En recevant une information (par exemple, un nom de domaine visité par untel), chaque algorithme en tirera une liste de briques à peindre en jaune. Les briques sont colorées ainsi de suite à chaque arrivée d’une nouvelle donnée. Bien évidemment, passer un coup de peinture à un endroit déjà peint ne change rien.

Pour savoir si telle information a été mise dans le mur ou non, il suffit de demander aux algorithmes : « Si je vous avais donné telle information à traiter, vous auriez peint quelles briques ? ».

• Si ces briques-là sont peintes, l’information a probablement été mise dans le mur ; mais il est possible que ce soit une coïncidence et que les briques aient été peintes pour autre chose, et ce d’autant plus que le mur est petit.
• Si au moins une de ces briques-là est blanche, on peut être sûr à 100% que l’information n’est pas dans le mur.

Avec Google, un mur de briques est peint chez chaque utilisateur. Pour rajouter en sécurité, on injecte du bruit de la même manière que ce que vous avez déjà vu : une fonction probabiliste arrive avec deux pots de peinture, un blanc et un jaune, et décide au hasard de repeindre certaines briques, en tirant le choix de la couleur à pile ou face. Le mur peut alors être envoyé à Mountain View, où il est décodé de manière tout aussi complexe.

Conclusion

La confidentialité différentielle est quelque chose de réel et de mathématiquement démontrable. C’est cependant dans son implémentation que la prudence doit être de mise ; et là, comme souvent en cryptographie, l’open source est une force. Il contraint les cryptographes à construire des procédés solides au lieu de miser sur l’ignorance des attaquants, et permet, comme dans le logiciel libre, que les algorithmes soient passés en revue par quiconque a les compétences pour.

comme souvent en cryptographie, l’open source est une force

Apple n’est pas si fermé qu’on peut le croire : en témoigne le système open source Darwin OS, entretenu depuis plus de quinze ans comme base de tous les systèmes Apple et ayant même une distribution GNU-Darwin (c’est dire !). Sa mascotte ornithorynque résonne pourtant comme un clin d’œil à l’attitude contradictoire de la firme de Cupertino sur le sujet. On ne peut qu’espérer que celle-ci publiera comme Google ses algorithmes de confidentialité, sans quoi le doute sur leur fiabilité restera toujours.

CC lux.musica.khaos

Votre VPN préféré n'est pas celui que vous croyez Quel est le meilleur VPN en 2024 ? Notre comparatif Retrouvez notre comparateur pour choisir le meilleur VPN