Un million de dollars seront offerts à toute personne qui réussira à résoudre l’une de ces énigmes mathématiques. En 2000, l’Institut de mathématiques Clay a posé sept problèmes, qui ont la réputation d’être insurmontables. À ce jour, seul l’un d’eux a été résolu.
Quels sont ces problèmes du prix du millénaire ? Et quel genre de réponse est attendue ? Démonstrations, équations, vérification d’une hypothèse… Si vous trouvez ne serait-ce que l’une des solutions, elle pourrait vous rendre riche — mais pour cela, il faut d’abord comprendre l’énoncé du problème, ce qui n’est pas toujours facile.
L’hypothèse de Riemann
Depuis 161 ans, l’hypothèse du mathématicien Georg Friedrich Bernhard demeure intacte. En 1858, il publie un article scientifique intitulé « Sur le nombre de nombres premiers inférieurs à une taille donnée ». Georg Frierich Bernhard s’y intéresse aux nombres premiers. On utilise ce terme pour qualifier un entier naturel (positif, qui permet de dénombrer) qui n’a pour seuls diviseurs que 1 et lui-même.
Prédire les nombres premiers est complexe. Comme l’explique Interesting Engineering, ils ne semblent suivre aucun modèle. Identifier un nombre premier ne permet pas de prédire le suivant. Il faut étudier d’autres nombres entre temps. Pour résoudre ce problème, Georg Frierich Bernhard a cherché à étudier les nombres premiers dans l’autre sens : peut-on prédire les nombres entiers plus petits qu’un nombre entier donné ?
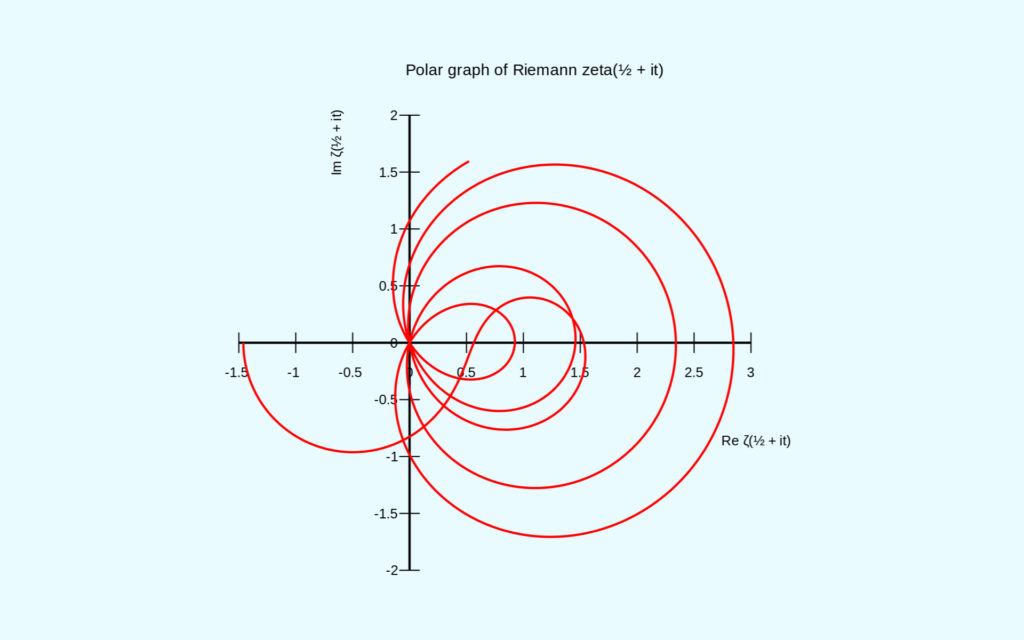
Le mathématicien a créé la fonction zêta de Riemann. D’après lui, la fréquence des nombres premiers est très proche de cette fonction. « L’hypothèse de Riemann affirme que toutes les solutions intéressantes de l’équation se situent sur une certaine ligne droite verticale », explique l’institut de mathématiques Clay. Les 10 000 000 000 000 premières solutions de l’équation ont été vérifiées. Mais ensuite ? Vérifier que l’hypothèse est toujours vraie permettrait d’en savoir davantage sur la distribution de ces nombres premiers.
Le problème P=NP
« S’il est facile de vérifier que la solution d’un problème est correcte, est-il aussi facile de résoudre le problème ? » : voilà comment l’Institut de mathématiques Clay résume le problème P=NP. Vous pouvez espérer un million de dollars si vous parvenez à démontrer que P=NP, que P≠NP ou qu’il n’existe aucune démonstration possible. Mais en quoi consiste cette énigme ?
L’institut propose un exemple pour comprendre. Vous avez un groupe de 400 étudiants à loger, avec un nombre de places limité. Seuls 100 étudiants pourront obtenir une place. Par ailleurs, vous avez une liste de paires d’étudiants qui ne sont pas compatibles : aucune des paires de cette liste ne doit apparaître dans la liste finale des étudiants.
Dans cette situation, vous pouvez vérifier facilement si une liste de 100 étudiants remplit ces critères. Néanmoins, « générer une telle liste à partir de zéro semble être si difficile qu’elle est tout à fait irréaliste », explique l’institut. Le nombre de façons de choisir les 100 étudiants parmi les 400 est plus élevé que le nombre d’atomes connus dans l’univers. Si vous réussissez à montrer qu’il existe bien des problèmes dont la solution peut être vérifiée rapidement, mais qui sont trop longs à résoudre, le million de dollars sera à vous.
L’équation de Navier-Stokes
Il s’agit en fait de plusieurs équations. Elles décrivent le mouvement des fluides, comme l’eau et l’air. Le challenge consiste à trouver les solutions de ces équations et à vérifier qu’elles sont uniques. Les équations ont été nommés ainsi pour rendre hommage à deux scientifiques du 19e siècle, Henri Navier et Goerge Gabriel Stokes.
« Les vagues suivent notre bateau alors que nous nous frayons un chemin à travers le lac et des courants d’air turbulents nous suivent en vol à bord d’un jet moderne », illustre l’Institut de mathématiques Clay. Comment prédire cette brise et ces turbulences ? La résolution des équations de Navier-Stokes est peut-être la solution.
Actuellement, seules des résolutions approchées sont utilisées, notamment par des météorologistes, pour comprendre les courants océaniques et les mouvements d’air dans l’atmosphère.
La conjecture de Hodge
Le mathématicien écossais William Hodge a formé cette conjecture au 20e siècle. Elle porte sur la géométrie algébrique et part du principe que des structures géométrique ont « une contrepartie algébrique », comme l’explique IFL Science. Cette dernière peut servir d’intermédiaire pour étudier les formes en question.
Pour comprendre ce dilemme, il faut faire un peu d’histoire. En 1637, Descartes montre comment la géométrie, devenue de plus en plus complexe, peut être exprimée sous forme algébrique — autrement dit, que l’observation géométrique et les calculs peuvent aboutir au même résultat. Quelques siècles plus tard, des objets géométriques ont ainsi été définis à partir de l’algèbre : on les appelle variétés algébriques. Si bien que certaines équations ont commencé à devenir particulièrement complexes à représenter sous forme géométrique.

La conjecture concerne des objets géométrique complexes à visualiser.
Source : Pxhere (photo recadrée)Comme l’explique la mathématicienne Claire Voisin, cette conjecture permet de lier des domaines différents des mathématiques. « La conjecture n’a pas d’application concrète prévisible comme les autres problèmes du millénaire, mais elle a permis d’impulser de nouveaux champs de recherche », note la spécialiste. Encore faut-il espérer la démontrer : William Hodge en avait eu l’idée, mais n’était pas parvenu à la vérifier.
La conjecture de Birch et Swinnerton-Dyer
Cette autre conjecture porte sur les courbes elliptiques. Selon l’Institut de mathématiques Clay, ce sont « des objets mathématiques fondamentaux qui apparaissent dans de nombreux domaines » (elles servent par exemple à décrire le mouvement des toupies).
L’institut rappelle que les mathématiciens ont cherché à trouver toutes les solutions possibles pour des nombres entiers, par exemple x, y ou z dans l’équation suivante (résolue par Euclide) : x²+y²=z². On parle d’équation diophantienne, car les solutions sont proposées parmi les nombres entiers. Mais que se passe-t-il lorsque les équations deviennent plus complexes ?
Bryan John Birch et Peter Swinnerton-Dyer, deux mathématiciens britanniques, ont proposé leur conjecture pour tenter des trouver des points sur des courbes elliptiques. Pour l’instant, la conjecture n’a été démontrée que sur des cas précis. Tout l’enjeu est de montrer qu’elle est toujours valable.
Les équations de Yang-Mills
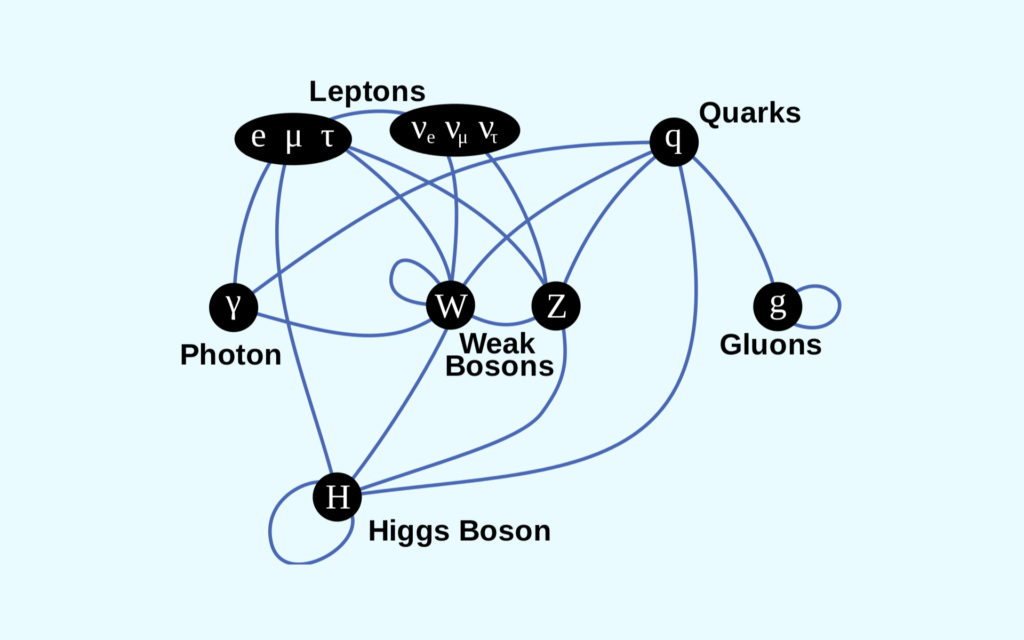
Les mathématiciens Chen-Ning Yang et Robert Willis ont établi cette théorie pour rendre compte d’un phénomène physique. Ce cadre sert à « décrire les particules élémentaires à l’aide de structures également présentes en géométrie », explique l’Institut de mathématique Clay.
De nombreuses théories sur les particules éléments ont pour base ce cadre, vérité en laboratoire. Mais ses fondements mathématiques sont bien plus obscurs. La difficulté vient de « l’écart de masse », qui n’a pas encore été expliqué théoriquement. La résolution de ces équations pourrait potentiellement guider les scientifiques vers de nouveaux concepts fondamentaux en physique et mathématiques, selon l’institut.
La conjecture de Poincaré (résolue)
C’est le seul des problèmes du prix du millénaire qui a été résolu. La conjecture de Poincaré a été démontrée en 2003 par Grigori Perelman, un mathématicien russe. Presque un siècle plus tôt, en 1904, le mathématicien français Henri Poincaré la mettait au point pour tenter de mieux comprendre des formes à trois dimension, et notamment la « sphère de dimension trois » ou « 3-sphère ».
« Poincaré s’est demandé s’il existait un test permettant de reconnaître le fait qu’une forme soit la 3-sphère en effectuant des mesures et d’autres opérations à l’intérieur de la forme », expliquait l’Institut de mathématiques Clay dans son communiqué annonçant la résolution de la conjecture.
Les travaux de Poincaré auraient pu devancer Einstein et son travail sur la relativité. Il s’intéressait à la stabilité du système solaire, se demandant si les planètes et astéroïdes restaient continuellement sur leurs orbites (ou s’ils pourraient être éjectés au fin fond de la galaxie).
Ironie de l’histoire : Grigori Perelman a refusé la récompense décernée par l’Institut de mathématiques Clay pour la résolution de cette conjecture. Il n’a pas récupéré le million de dollars qui l’attendait. Auparavant, il avait aussi refusé un prix de la Société mathématique européenne, ainsi que la médaille Fields.
+ rapide, + pratique, + exclusif
Zéro publicité, fonctions avancées de lecture, articles résumés par l'I.A, contenus exclusifs et plus encore.
Découvrez les nombreux avantages de Numerama+.
Vous avez lu 0 articles sur Numerama ce mois-ci
Tout le monde n'a pas les moyens de payer pour l'information.
C'est pourquoi nous maintenons notre journalisme ouvert à tous.
Mais si vous le pouvez,
voici trois bonnes raisons de soutenir notre travail :
- 1 Numerama+ contribue à offrir une expérience gratuite à tous les lecteurs de Numerama.
- 2 Vous profiterez d'une lecture sans publicité, de nombreuses fonctions avancées de lecture et des contenus exclusifs.
- 3 Aider Numerama dans sa mission : comprendre le présent pour anticiper l'avenir.
Si vous croyez en un web gratuit et à une information de qualité accessible au plus grand nombre, rejoignez Numerama+.
Toute l'actu tech en un clin d'œil
Ajoutez Numerama à votre écran d'accueil et restez connectés au futur !

Tous nos articles sont aussi sur notre profil Google : suivez-nous pour ne rien manquer !